Volume Shifts and Specific Gravity
Definitions and Relationships
Specific Gravitry
The specific gravity of a liquid is defined as the ratio between the liquid density and the liquid density of water at surface conditions (15C and 1 atm). The mathematical definition is given by
where \(\gamma\) is the specific gravity, \(\rho\) is the liquid density at surface conditions, and \(\rho_{water}\) is water density at surface conditions. Since the densityof water at surface conditions is approximately 1000 kg/m3, then the specificc gravity is approximately equal to the liquid density with units of g/cm3.
Volume Shift Factor
What makes the Peneloux et al. volume shifts so smart!
What makes the Peneloux et al. volume shift concept so breilliant is that it fixes the issue of poor component liquid density for the PR and SRK EOS models with a simple constant translation, that doesn't impact the vapor pressure calculation, and only has a negligible effect on the gas density prediction!
where \(v = V/n\) is the actual molar volume, \(v^{EOS}\) is the EOS calculated molar volume, \(s_i\) is the unitless volume shift, \(c_i\) is the volume shift with units, \(b_i\) is the EOS component parameter (also called co-volume), \(V\) is the volume, and \(n\) is the mole amount.
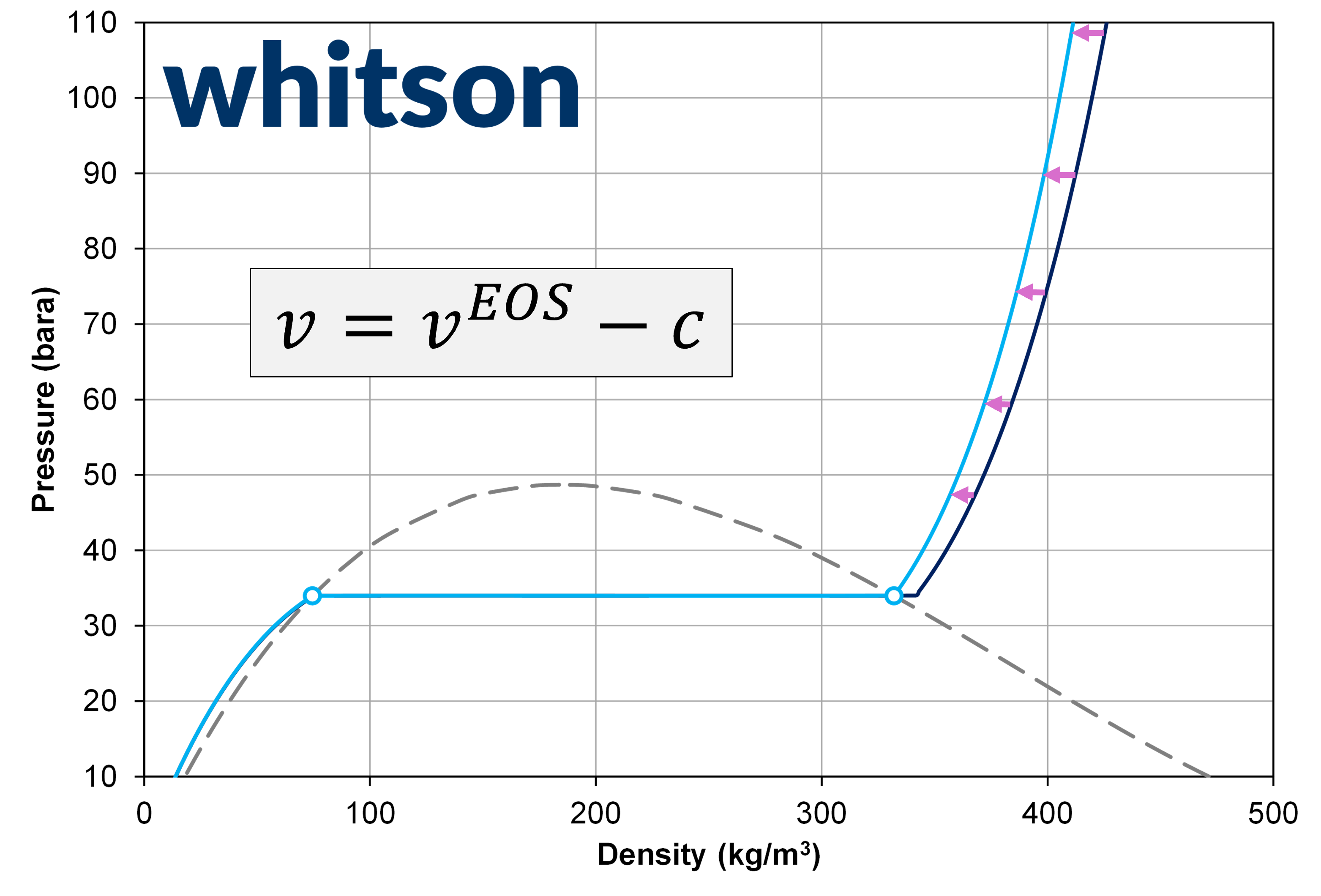
Figure 1: Example of pressure-density relationship for ethane (C2) with a unitless volume shift value of 0 (dark blue) and 0.099 (light blue).
Relationship
Similar to the relationship between acentric factor and normal boiling point, it is only possible to have a single consistent relationship between the component specific gravity and component volume shift. This means that there is just one volume shift that will give an exact match of the component liquid specific gravity!
Volume Shift Factor from the Specific Gravitry
As mentioned in the previous section, there is only a single volume shift that honors the component liquid specific gravity. Using this fact, you can estimate the volume shift by iteration to honor the component liquid specific gravity, resulting in accurate stock tank oil density predictions, given that the C7+ characterization has been done correctly!
Note from Curtis from the SPE Monograph Phase Behavior
Peneloux et al. propose that ci be determined for each component separately by matching the saturated-liquid density at Tr = 0.7. ci can actually be determined by matching the EOS to any density value at a specified pressure and temperature.
Volume Shift Factor from Correlations
It is also possible to estimate the volume shifts from correlations. One exampole of this is given in the next section, but the reader should be advised that these estimated values might not honor the C7+ characterization data.
Jhaveri and Youngren
where \(s_i\) is the unitless volume shift, \(c_i\) is the volume shift with units, \(b_i\) is the EOS component parameter (also called co-volume), and \(M_i\) is the component molecular weight.
The values for \(A_0\) and \(A_1\) are given below.
| Hydrocarbon Family | A0 | A1 |
|---|---|---|
| Paraffins | 2.258 | 0.1823 |
| Naphthenes | 3.004 | 0.2324 |
| Aromatics | 2.516 | 0.2008 |