Acentric Factor and Normal Boiling Point
Definitions and Relationships
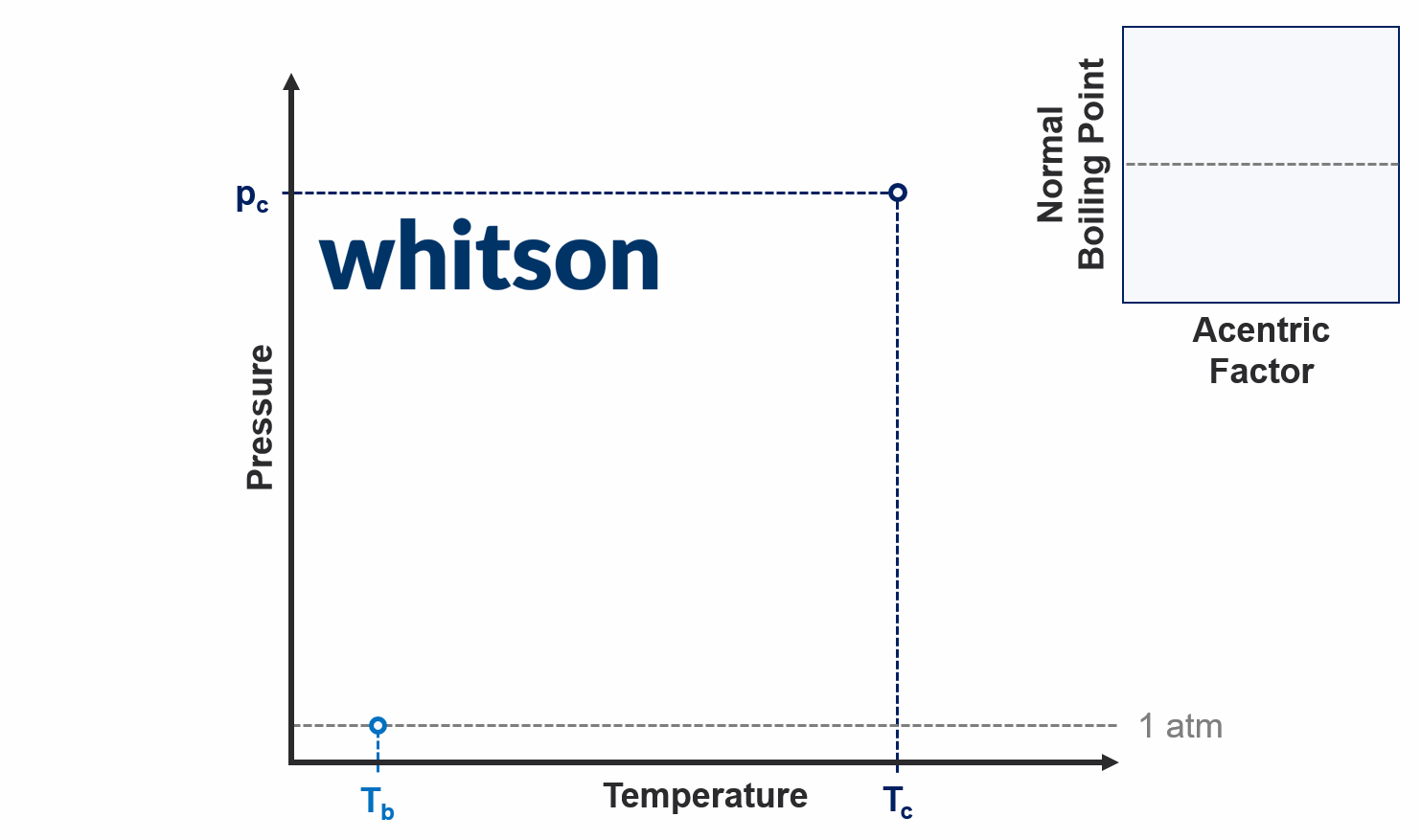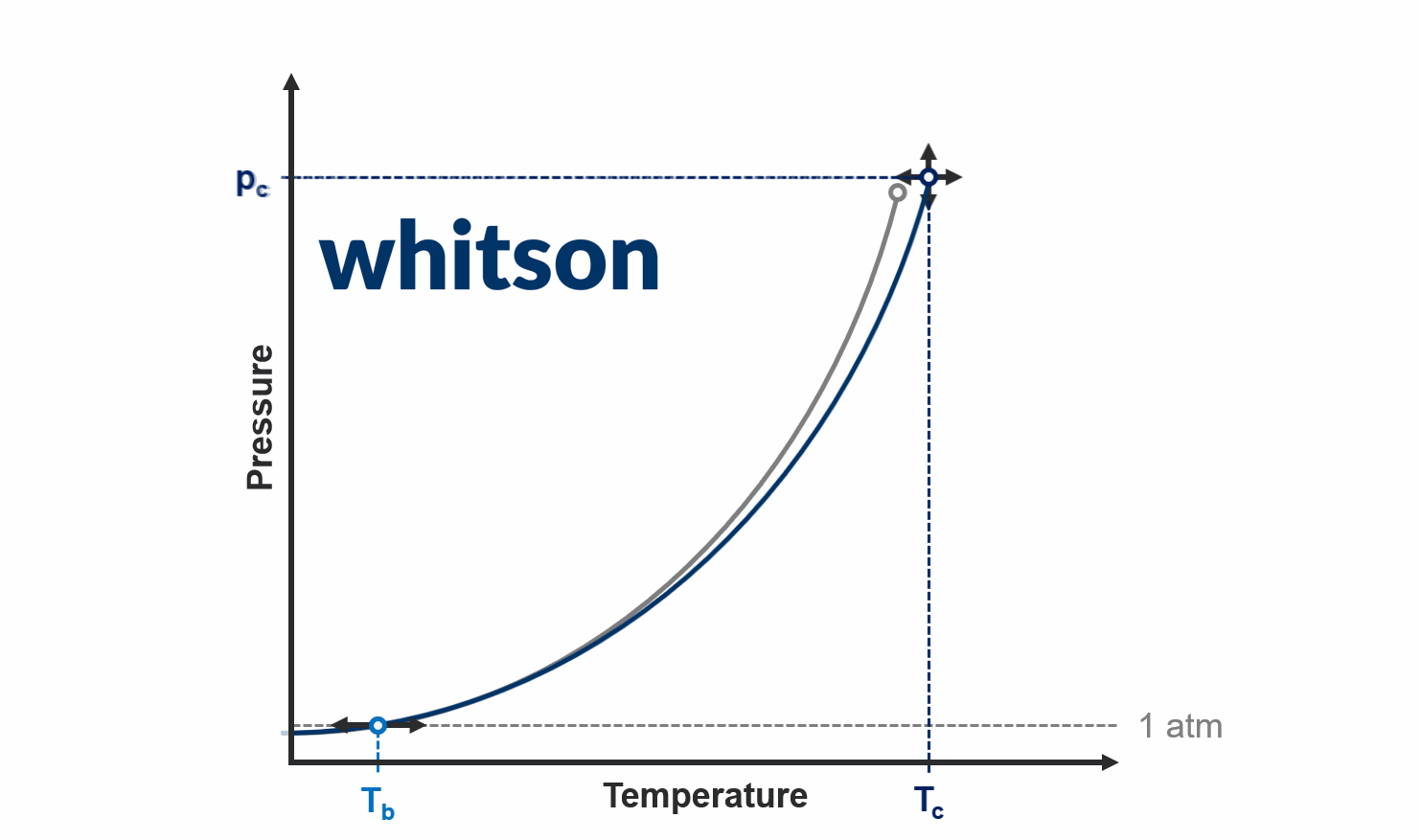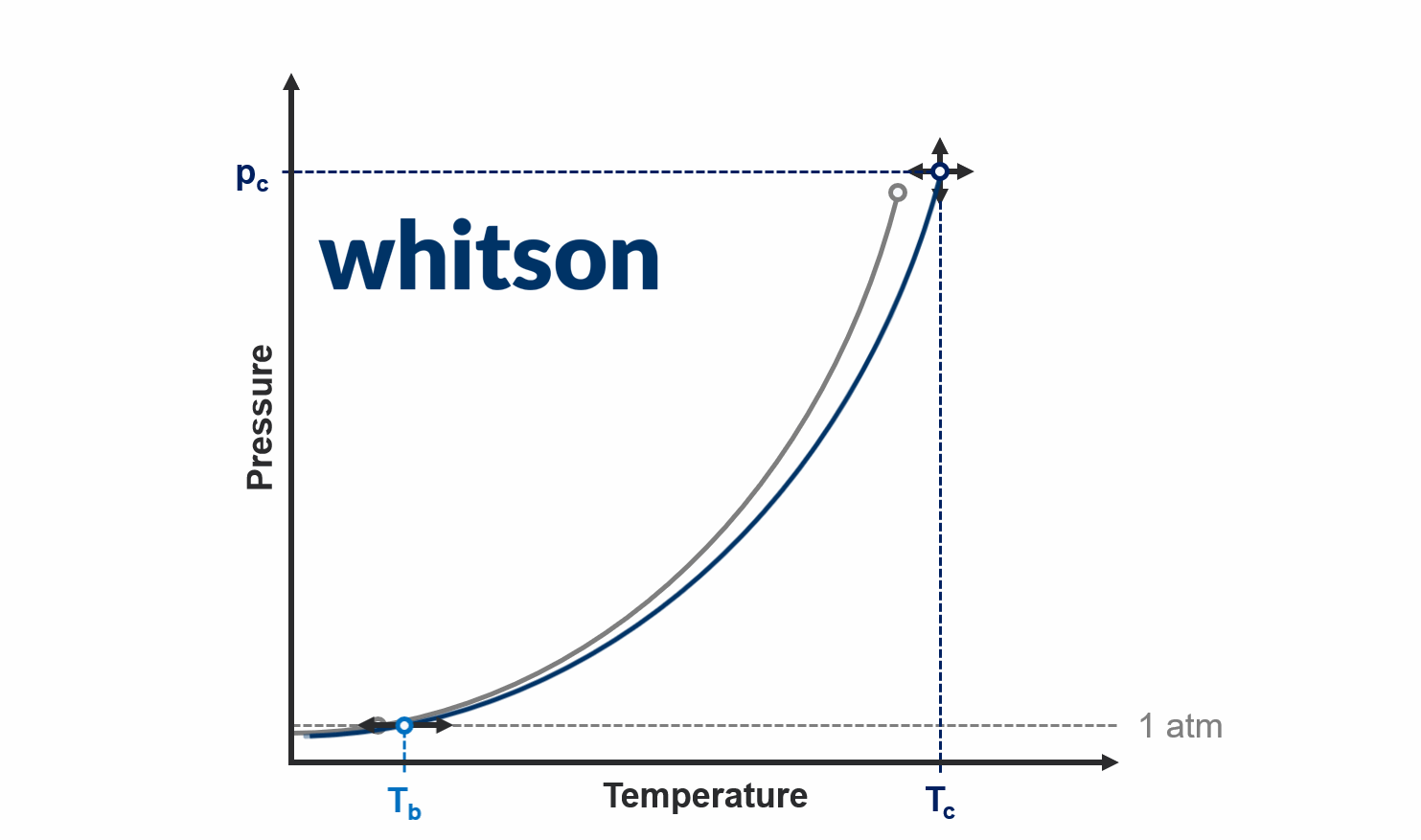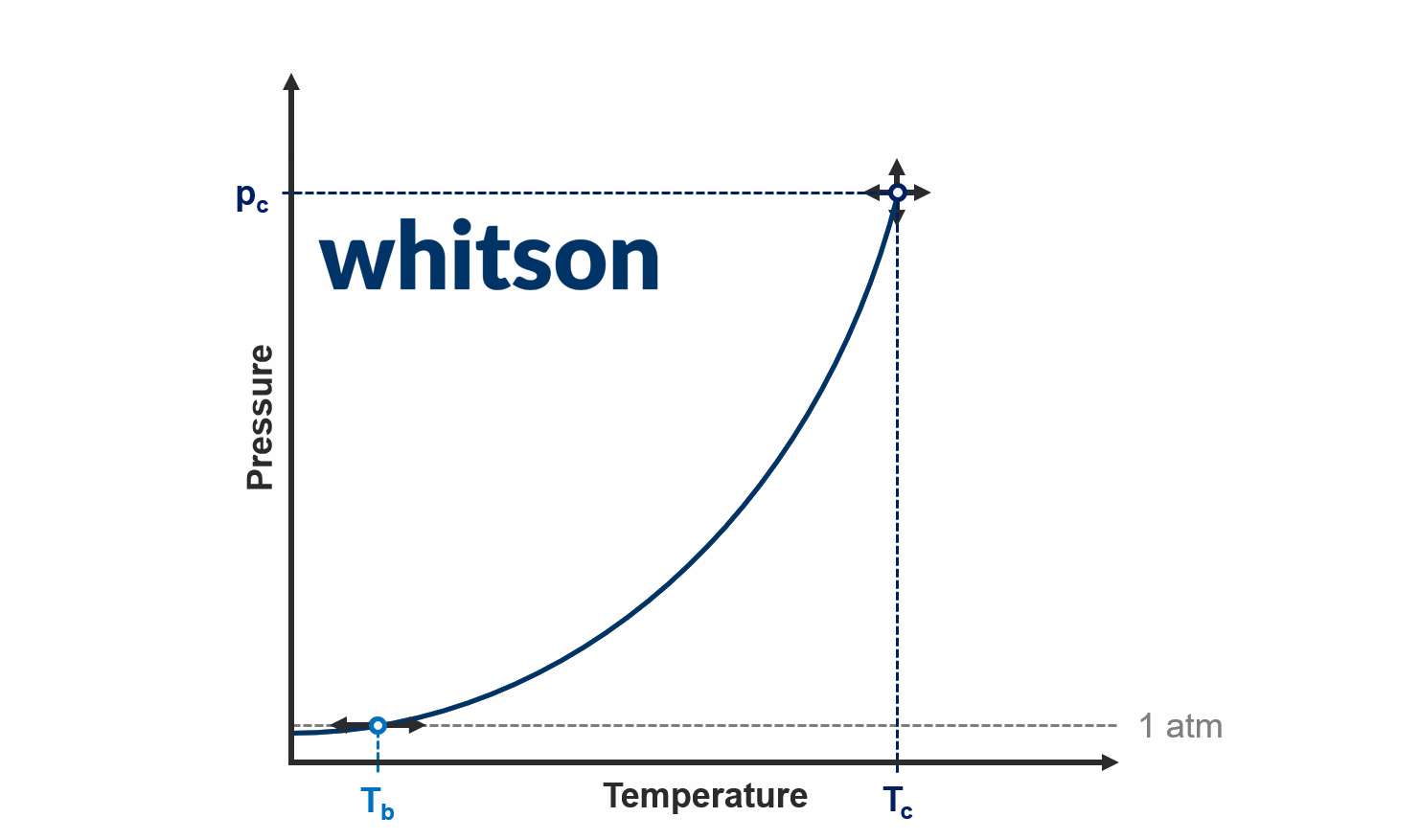
Normal Boiling Point
The mathematical formulation of the normal boiling point is given by
Acentric Factor
The mathematical definition of the acentric factor (ω) is given by
where \(T^* = 0.7\cdot T_c\) (temperatures in absolute units), \(p_v\) is the vapor pressure, \(p_c\) is the critical pressure, and \(T_c\) is the critical temperature.
Relationship
Both the acentric factor and normal boiling points are tied to a point on the vapor pressure curve at conditions below the critical point. There is a one-to-one relationship between the acentric factor and normal boiling point, meaning that there is only one acentric factor that honers the critical point and a given normal boiling point, and vice versa. This relationship is shown in Figure 1 below, and shows what acentric factors result in a ± 10C shift in the normal boiling point.
Since the normal boiling point is the defining bound for single carbon number components, it is a physical constraint that should be honored. This is the reason why, in whitsonPVT, there is no regression on the acentric facotrs, but rathre on the normal boiling points.
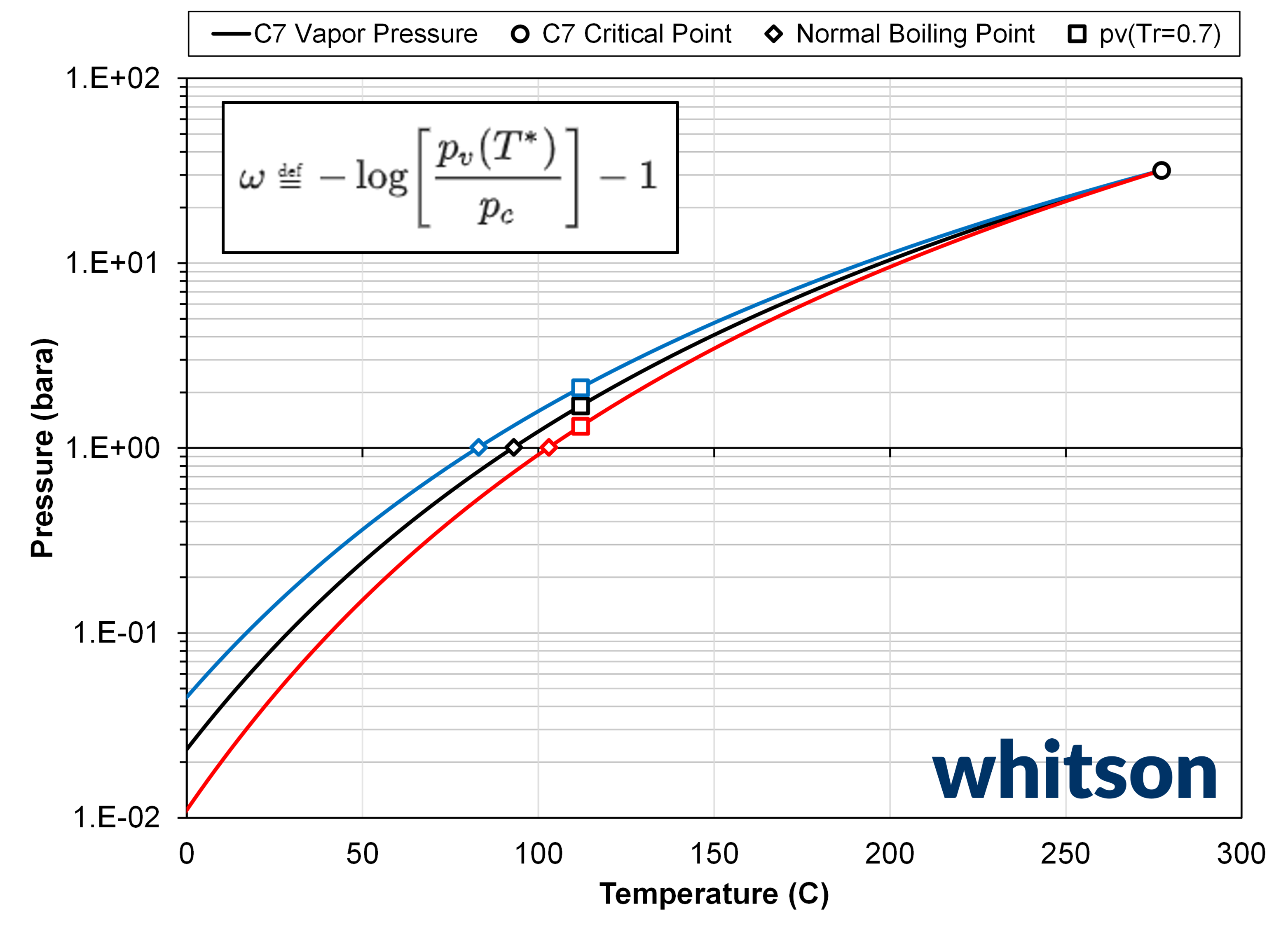
Figure 1: Figure showing the vapor pressure line (solid lines), critical point (circle), normal boiling points (square symbols), and the vapor pressure at Tr = T* / Tc = 0.7 for three EOS models where (ω, Tb) = (0.27056, 93.197C) (black), (ω, Tb) = (0.17378, 83.197C) (blue), and (ω, Tb) = (0.38288, 103.197C) (red). The component is a SCN C7 component and the EOS is a PR78 model with volume shifts.
Acentric Factor from the Normal Boiling Point
The only accurate method honor both the normal boiling point and critical point for a given component is to solve for the acentric factor iteratively until the vapor pressure at the normal boiling point temperature is equal to atmospheric pressure! This is shown in the animation below.
Acentric Factor from Correlations
Approximate values for the acentric factor can be estimated from correlations. The Lee-Kesler and Edmister models utilize the component normal boiling points to estimate the acentric factor, making it a bit more accurate, but the Pedersen model does not!
Acentric factor correlations do NOT honor the normal boiling points!
It is important to note that these values do not honor the normal boiling point exactly and will impact the EOS calculated normal boiling points!
Lee-Kesler Model
The Lee-Kesler correlation for acentric factors aims to convert the normal boiling point to a reasonable estimate for the acentric factor. The correlation is given by
and
where \(T_{br} = T_b / T_c\) is the reduced normal boiling point, \(K_w\) is the component Watson factor, and the coefficients are given below. The temperature units are in absolute values.
Table 1: Coefficients for the Lee-Kesler acentric factor model.
| Coefficient | Value |
|---|---|
| A1 | -5.92714 |
| A2 | 6.09648 |
| A3 | 1.28862 |
| A4 | -0.169347 |
| A5 | 15.2518 |
| A6 | -15.6875 |
| A7 | -13.4721 |
| A8 | 0.43577 |
Edmister Model
where \(p_c\) is the critical pressure, \(T_c\) is the critical temperature, \(p_{sc}\) is the surface pressure, \(T_b\) is the normal boiling point. The temperature units are in absolute values.
Pedersen Model
where \(m(\omega)\) is the slope in Soave's correction term (\(\alpha(T)\)) to the EOS a parameter, \(\omega\) is the component acnetric factor, \(M\) is the component molecular weight, \(\rho\) is the component liquid viscosity at surface conditions. The equations for \(m(\omega)\) for the PR EOS can be found here, and for the SRK EOS can be found here.
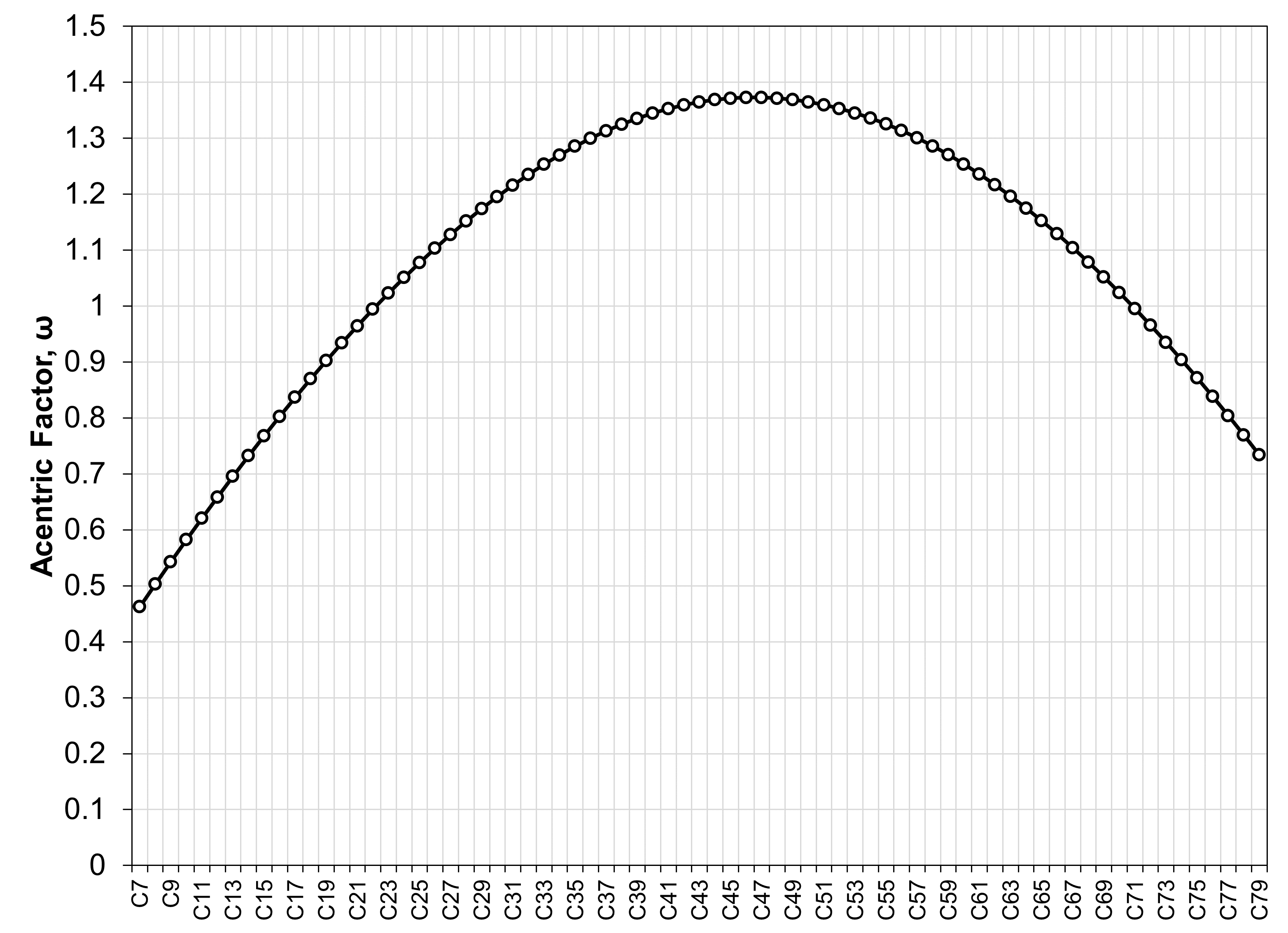
Non-physical component acentric factors
The acentric factors using the Pedersen model are non-monotonic for heavier SCN components, resulting in non-physical thermodynamic behavior! This is shown in the figure below using the Pedersen model with the PR EOS model.
Parameters for SRK and PR EOS models
| EOS Type | e1 | e2 | e3 | e4 |
|---|---|---|---|---|
| SRK | 0.74310 | 4.8122e-3 | 9.6707e-3 | -3.7184e-6 |
| PR | 0.373765 | 5.49269e-3 | 1.17934e-2 | -4.93049e-6 |
Excel Test File
We at whitson have made an Excel file with all the correlations above, that you can download for free here.